Definiciones

El objetivo de esta práctica es utilizar el programa Geogebra para construir mosaicos y repasar algunos conceptos de Geometría.

Antes de comenzar, es conveniente repasar algunos conceptos que vamos a usar a lo largo de toda la práctica: Los movimientos en el plano. 

1) Un giro  de centro O y ángulo α , transforma todo punto P en otro P' tal que OP = OP' y el ángulo POP' = α

Si el centro de giro sobre el que aplicamos la trasformación es el centro geométrico de la figura, entonces se trata de una rotación.

Una figura es SIMÉTRICA POR ROTACIÓN si al girarla un determinado ángulo (distinto de 360º), alrededor del centro de rotación O, la figura vuelve a su posición inicial.

En la figura siguiente es evidente que el centro de rotación es el centro del hexágono, pero ¿qué ángulos hemos de rotarla para que coincida consigo misma ? 

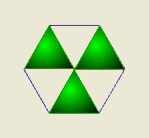
Debemos rotarla 120º y 240º, como se muestra en la animación siguiente :

Se llama ORDEN de ROTACIÓN (n) al número de veces que hay que rotar el ángulo menor (α) para dar una vuelta completa  (n = 360º/ α) o, al número de figuras idénticas que forman la figura completa.

La figura anterior es de orden de rotación 3.

Veamos otro ejemplo : 

El centro de rotación es el centro del cuadrado, los ángulos de rotación son 90º, 180º y 270º y el orden de rotación es 4 

Antes de pasar a la isometría siguiente, practica un poco las rotaciones con Cabri en esta página y con Geogebra en esta otra.

2) Una traslación determinada por un vector v transforma a todo punto P en otro P' tal que el vector PP' = v.

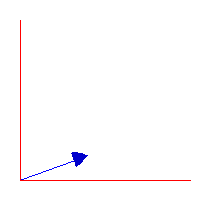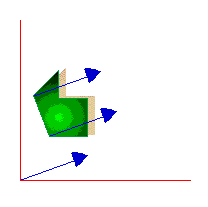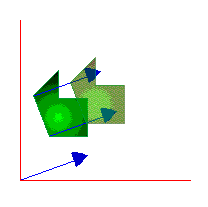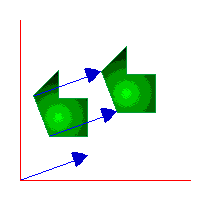
Ahora practica unas traslaciones en esta página o en esta otra.

3) Una simetría respecto de un eje de simetría e, transforma a todo punto P en otro punto P' tal que el eje (e) es mediatriz del segmento PP'. Es una reflexión.

Ahora puedes practicar las reflexiones en esta página  o en esta otra .

Podemos considerar una cuarta isometría que es una composición o producto de dos de las anteriores de manera que cualquier isometría del plano puede explicarse por la combinación de estas cuatro. 

4) Reflexión con deslizamiento que consiste en una composición de dos las isometrías anteriores, una reflexión respecto de un eje e seguida de una traslación según un vector v ( o viceversa) :

Para terminar una práctica sobre deslizamientos en esta página.

Los movimientos pueden ser directos (cuando se conserva el sentido de giro de las figuras) como las traslaciones y giros, o inversos (si no se conserva el sentido de giro de las figuras) como en las simetrías axiales.

Las isometrías de los polígonos se estudian, con Geogebra y Flash, en esta página.

Imprime esta página e indica las traslaciones y reflexiones que encuentras en los mosaicos semirregulares.

La composición de dos isometrías se estudian en esta página.

Las isometrías desde el punto de vista analítico se estudian en esta página .

Ahora daremos algunas definiciones básicas previas:

- Figura: Cualquier dibujo en el plano.

- Diseño: En general se considera un diseño cualquier figura con alguna isometría (distinta de la identidad, que siempre tiene).

- Clasificación de los diseños

(1) Diseños finitos o discretos: Aquellos diseños que poseen un centro o ejes de giro alrededor de los cuales sus elementos constituyentes pueden rotar, pero carecen del resto de las isometrías (traslaciones, simetrías axiales o deslizamientos). Se pueden clasificar en dos clases:

(1.1) Grupos con centro de giro de orden n (denotados por c(n)) o rotacionales: Tienen un centro de giro de orden n, girando (en sentido horario o antihorario) n veces 360º/n grados se vuelve al motivo inicial.

(1.2) Grupos con n ejes de simetría centrales (denotados por d(n)) o diedricos : El motivo se refleja n veces respecto de n ejes centrales de simetría que forman ángulos de 360º/n grados.

En la figura siguiente puede verse la diferencia si a un mismo motivo (en azul) se le aplica un grupo c(6) o d(6):

Estudiaremos más sobre este tipo de diseños en esta página.

(2) Diseños traslacionales: Decoran el plano por repetición regular de un motivo mediante traslaciones de su celda unidad. Pueden clasificarse en dos tipos dependiendo que de que la traslación sea en una sola dirección del plano (la horizontal normalmente), son los diseños monotraslacionales (frisos, celosias o cenefas) o que traslademos el motivo en las dos direcciones del plano, son los ditraslacionales (mosaicos, que, en principio, era el objeto de este trabajo)

Rejilla, malla o trama:

Un conjunto de puntos que forman una red o enrejado regular entre líneas paralelas, es una rejilla o trama.

Celdilla unidad:

Cada uno de los paralelogramos que forman una trama, red o malla. Hay cinco tipos de celdillas unidad .

Unidad de traslación:

Es el área mínima del plano que mediante traslaciones sucesivas (en una dirección, para los frisos, o las dos direcciones del plano, para los mosaicos) genera el diseño completo. Tiene el mismo área que la celdilla unidad pero no tiene por que tener la misma forma, ni tan siquiera ser una paralelogramo. Toda celdilla unidad constituye una unidad de traslación pero lo contrario no tiene porqué ser cierto. Los lados opuestos de una unidad de traslación deben ser paralelos pero no tienen porqué ser líneas rectas.

Dominio Fundamental, loseta básica, celda base o región generadora:

El área o región del plano que al aplicarlas las isometrías del grupo de simetrías a que pertenece genera el diseño completo. La forma de la loseta básica puede no ser única para un diseño dado pero su área sí ha de ser la misma. 

En los siguientes diseños puede apreciarse la diferencia entre los tres últimos conceptos definidos:

En un friso:

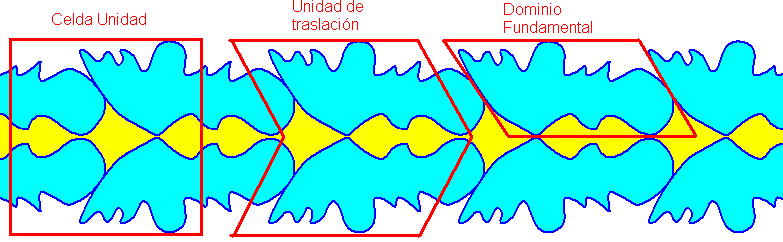
Y en un mosaico:

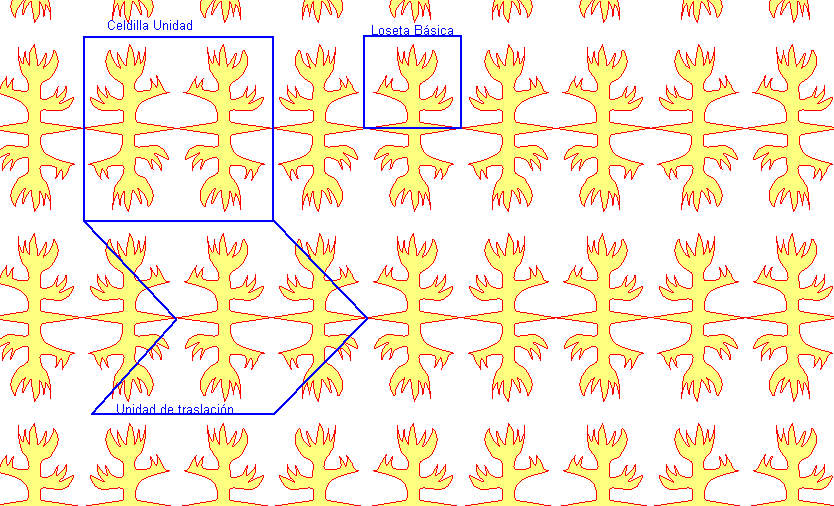
Si necesitas imprimir mallas o rejillas ve a esta página.

Notación:

Se suelen usar tres sistemas de notación distintos para nombrar (y distinguir) los grupos de simetría del plano:

(1) Cristalográfica:

(a)Completa

(b)Abreviada

(2) Fejes Tóth.

(3) Por orbifold.

Aunque excede los objetivos de esta practica, para quienes deseen profundizar se exponen, sucintamente, en esta página.