Vamos a hacer unas practicas de construir mosaicos variando los tamaños basados en polígonos regulares.
1) Con triángulos equiláteros
Si comenzamos con la situación más sencilla, la relación entre las longitudes de los lados 1/2, se forma el mosaico:
Relación entre los lados 1/2
Si la relación es de 1/3, tenemos :

Relación entre los lados 1/3
Una relación de 2/3 nos daría un mosaico como :

Relación entre los lados 2/3
Imprime el cuestionario y contesta a las preguntas del apartado triángulos.
2) Con cuadrados
Si la longitud de los lados de los cuadrados están en la relación 1/2, además de la colocación casi inmediata:

Cuadrados en relación entre los lados 1/2
pueden darse otras configuraciones :

Cuadrados en relación entre los lados 1/2

Cuadrados en relación entre los lados 1/2

Cuadrados en relación entre los lados 1/2

Cuadrados en relación entre los lados 1/2
Algún ejemplo animado:
Para terminar un mosaico parecido al anterior pero con la longitud de los lados de los cuadrados en la relación 3/5:

Cuadrados en relación entre los lados 3/5>
Contesta a las preguntas del cuestionario impreso, relativas al apartado de los cuadrados.
3) Con hexágonos regulares y triángulos equiláteros
Un par de mosaicos con el lado del hexágono de longitud doble que la del triángulo :
El lado del hexágono mide el doble que el del triángulo
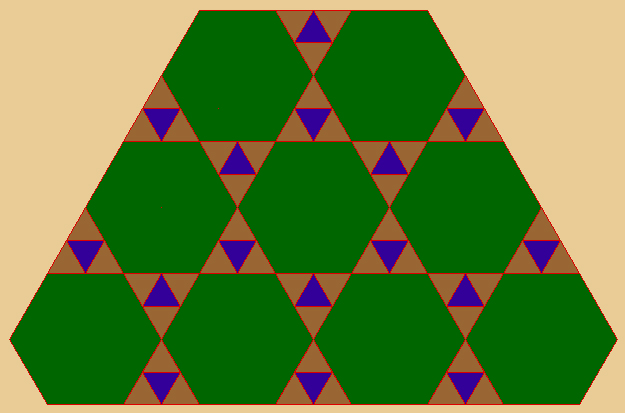
El lado del hexágono mide el doble que el del triángulo
Un ejemplo con la relación 1/3:

El lado del hexágono mide el triple que el del triángulo
Ahora un ejemplo al revés, la longitud del lado del hexágono la mitad de la longitud del lado del triángulo:
