Clasificación de triángulos

1) Atendiendo a la longitud de sus lados

Para comenzar, una actividad aparentemente fácil: Conseguir que cada triángulo sea del tipo que se indica, en los dos primeros (para facilitar la tarea) hemos incorporado deslizadores que varian las longitudes de los lados, en el escaleno has de conseguir las longitudes de los lados moviendo los vértices (¿a que no es tan fácil?).

Ahora te propongo que los dibujes usando Geogebra.

(1) Dibuja un triángulo equilátero de longitud del lado l =3

(i) Abrimos el programa Geogebra. Para que te sirva para otros triángulo equiláteros, añade un deslizador (a) (de intervalo de 1 a 10) que fijamos en el valor 3 que va a ser la longitud del lado de nuestro triángulo equilátero.

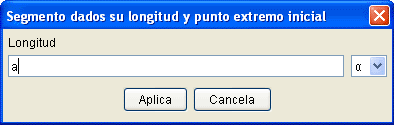
(ii) Dibujamos uno de los lados con la herramienta [Segmento dados su longitud y punto extremo inicial] , pulsamos en el punto incial y nos aparececerá una ventana en que hemos de introducir su longitud, introducimos a, que es como hemos llamado, por defecto, al deslizador que va a variar la longitud del lado:

(iii) Una vez que tenemos un lado (variable con el deslizador) dibujado, segmento AB, dibujamos, con la herramienta [circunferencia con centro y punto que cruza] dos circunferencias, una con centro en A y extremo en B y otra con centro en B y extremo en A.

(iv) El punto de intersección entre las dos circunferencias es el tercer vértice del triángulo equilátero, que marcamos con la herramienta [Intersección de dos objetos] . Después dibujamos el triángulo con la herramienta [Polígono] pulsando consecutivamente sobre los tres vértices del triángulo.

En la siguiente animación se muestran los pasos esenciales de la construcción que puedes visualizar moviendo el deslizador

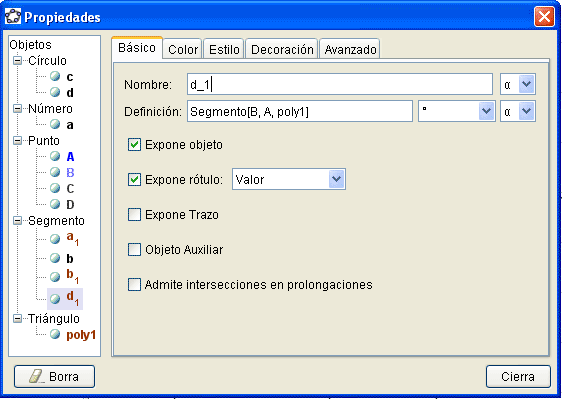
Para comprobar que es equilátero, mostramos las longitudes de sus lados: pulsamos con el botón derecho sobre cada lado para abrir el menú contextual, seleccionamos la opción [propiedades] y en la ventana emergente en el apartado [Expone objeto] seleccionamos [Valor] para que se nos muestre en dibujo la longitud de cada lado, en esta misma ventana podemos cambiar el color, el estilo y la decoración del objeto seleccionado (un segmento en nuestro caso):

Para comprobar los ángulos, usamos la herramienta [Ángulo] . Si pulsas sobre los tres vértices de cada ángulo de manera que el segundo se corresponda con el del ángulo a medir, se te dibuja el ángulo y su medida. Observa que si mueves el deslizador que has incorporado a tu dibujo, se obtienen triángulos equiláteros semejantes.

Una vez evidenciadas que son iguales las longitudes de los lados y las amplitudes de los ángulos guarda el archivo y mándalo por correo electrónico a tu profesor o envíalo a tu carpeta de trabajos correspondiente.

Pero ¿hay en Geogebra alguna otra forma de dibujar un triángulo equilátero de forma más rápida?, por supuesto, con la herramienta [Polígono regular] que está en el mismo grupo de la herramienta polígono .  Con la herramienta activada, pulsamos sobre los dos puntos que van a a formar un lado y se nos abre una ventana que nos pide el número de vértices (3 en nuestro caso), y se nos dibuja el triángulo (que podemos personalizar: color, trazo, sombreado, medidas,etc). Si pulsamos sobre cualquiera de los dos puntos iniciales y los modificamos (estirando o encogiendo el segmento) se modifican dinámicamente las longitudes de los lados.

Abre y contesta ahora al Cuestionario nº 4 y lo envías o guardas para ser corregido

Para terminar y cerrar este primer apartado de clasificación de triángulos te propongo que hagas con Geogebra un par de ejercicios más:

(2) Dibuja un triángulo isósceles cuyos lados midan 3 cm, 4 cm y 4 cm. (Aquí puedes refrescar el método de dibujo de triángulos dados sus lados).

Una vez dibujado etiqueta los vértices, mide los lados y archívalo con tu nombre e Isósceles en tu carpeta del servidor, para enviarlo posteriormente por correo a tu profesor

(3) Dibuja un triángulo escaleno cuyos lados midan 7 cm, 5 cm y 4 cm.

Una vez dibujado etiqueta los vértices, mide los lados y archívalo con tu nombre y Escaleno en tu carpeta del servidor, para enviarlo posteriormente por correo a tu profesor. 

2) Atendiendo a la amplitud de sus ángulos

Ya sabes que los tres ángulos interiores de cualquier triángulo suman 180º, una demostración visual muy común es cortar los picos del triángulo y juntarlos para comprobar que forman 180º, en la animación siguiente se muestra el proceso:

Otra demostración visual, más geométrica es:

Triángulos rectángulos. Teorema de Pitágoras

4) Dibuja un triángulo cuyos lados midan 5 cm, 4 cm y 3 cm y comprueba que es rectángulo

Sigue el procedimiento de la práctica de construcción de triángulos dados los tres lados y mide sus ángulos para comprobar que uno de ellos es recto, lo archivas con tu nombre y Rectangulo1 y contesta a las preguntas que se te formulan en el Cuestionario Nº 5 (no se te olvide imprimirlo, una vez resuelto, y/o entregarlo).

Comprobación de que en un triángulo rectángulo los ángulos agudos son complementarios y comprobación del teorema de Pitágoras

i) Incorpora dos deslizadores (de 0 a 10) que van a ser los catetos y dibuja un segmento AB de longitud el primer deslizador con la herramienta .

ii) Traza una [ Recta perpendicular ]al segmento por el extremo A.

iii) Dibuja una circunferencia de centro en A y radio el otro deslizador, la intersección de la circunferencia con la recta será el otro cateto.

iv) Dibuja el triángulo rectángulo y oculta la recta y la circunferencia.

v) Dibuja los ángulos y pon su amplitud, asi como la longitud de los lados.

vi) Marca y mide los ángulos (al marcar el de 90º, te saldrá la marca de ángulo recto). Deberás obtener algo similar a :

Si, en la animación anterior mueves los deslizadores para cambiar las longitudes de los catetos, podemos observar que :

- El ángulo A no se modifica, el triángulo sigue siendo rectángulo.

- La suma de los dos ángulos agudos tampoco varía. B + C = 90º, son complementarios.

- La hipotenusa al cuadrado y la suma de los cuadrados de los catetos sí varían pero permanecen iguales entre sí, teorema de Pitágoras (a² =b² + c²).

Guarda tu archivo como Pitagoras1 y envíalo por correo o cárgalo en Drive.

Otra comprobación del teorema de Pitágoras:

(i) Abre un archivo nuevo y sigue los pasos del ejercicio anterior para dibujar y etiquetar un triángulo rectángulo.

(ii) Dibujamos un cuadrado sobre cada uno de los lados mediante las herramientas [Polígono regular].

(iii) Hallamos las áreas de los cuadrados construidos sobre los tres lados mediante [Área].

(iv) Sumamos las áreas de los cuadrados construidos sobre los catetos (b² + c² ) y constatamos que es igual al área del cuadrado construido sobre la hipotenusa (a²) lo que demuestra el teorema :

Guarda este archivo con tu nombre y Pitágoras2.

Ahora dibuja un triángulo cualquiera y dibuja los cuadrados sobre los lados, estudia la relación entre las áreas al tiempo que contestas el Cuestionario Nº 6 .

En esta otra página puedes ver la generalización del teorema de Pitágoras y en esta otra tienes demostraciones dinámicas a modo de puzzles