Mosaicos en espiral

1) Mosaicos espirales basados en los radiales

Una forma de sencilla de conseguir teselación espiral es a partir de los mosaicos radiales construidos con triángulos. Si trasladamos (a derecha o izquierda) la mitad  inferior hacia la izquierda (o derecha) la distancia de una celda se obtiene un mosaico en doble espiral (enfrentadas):

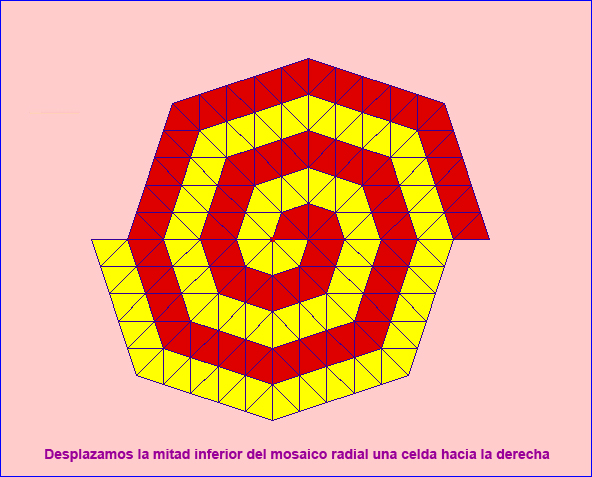
Mosaico espiral con triángulos

La mitad inferior está trasladada hacia la izquierda, pero puede trasladarse hacia la derecha y, si se modifican las dimensiones del triángulo original, hay que trasladar el centro de la mitad inferior para que coincidan las dos mitades en la diferencia de una celda.

Si en lugar de una celda, trasladamos la mitad inferior dos triángulos, se obtiene una doble espiral de doble rama:

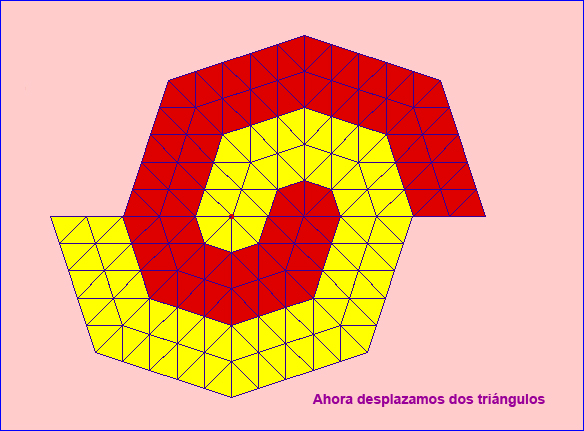
Mosaico en doble espiral con rama doble

Lo mismo puede hacerse con la espiral radial basada en rombos para lograr una teselación espiral de características especiales:

Teselación espiral con rombos

Si trasladamos el centro dos celdas base, se obtiene un doble espiral de doble rama:

Mosaico en doble espiral de doble rama con rombos

2) Mosaicos espirales basados en las espirales arquimedianas

También puede conseguirse teselación espiral basándonos en las espirales arquimedianas.

Con la espiral de Arquímedes:

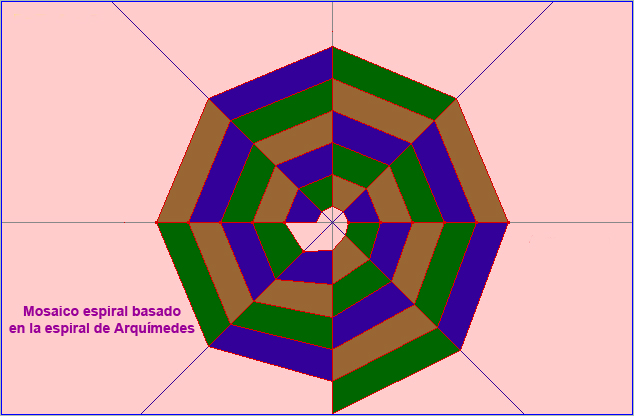
Mosaico basado en la espiral de Arquímedes

O una espiral de tres centros:

- Dibuja un triángulo equilátero ABC.

- Traza las semirectas que parten de sus vértices.

- Dibuja la circunferencia de centro en el vértice A y radio la longitud del segmento AB.

- Marca el punto D, intersección de la semirecta que pasa por A y la circunferencia anterior.

- Dibuja el primer arco de la espiral por los puntos B, C y D.

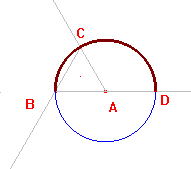
- Dibujamos otra circunferencia de centro en B y radio la longitud del segmento BD.

- El punto de intersección de esa circunferencia con la semirecta que pasa por B lo etiquetamos E.

- Dibuja el arco que pasa por los puntos D, un punto de la circunferencia y B.

Repetimos los pasos.

- Circunferencia de centro en C y radio CE.

- Punto F intersección de la circunferencia anterior con la semirecta que pasa por C

- Arco E, punto en circunferencia y punto F.

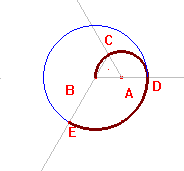
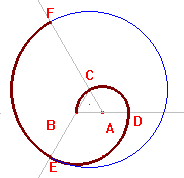
- Y así sucesivamente asta obtener la espiral, sobre la que trazamos sectores y dibujamos cuadriláteros para obtener una teselación espiral arquimediana.

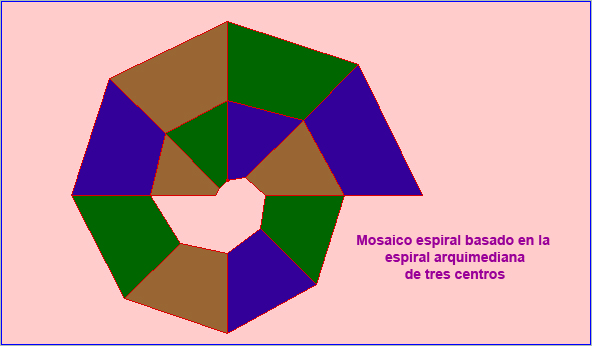
Mosaico en espiral basado en la espiral arquimediana de tres centros

3) Mosaico espiral basado en la espiral de Durero

La espiral descubierta por Durero se basa en el número áureo (F), por tanto vamos a comenzar por construir el rectángulo áureo:

(a) Conocido el lado menor

- Dado el lado menor AB, se dibuja un cuadrado ABCD de lado igual a la longitud del segmento AB.

- Por el punto medio (M) de uno de los lados del cuadrado (AD por ejemplo) con radio la distancia de este punto a uno de los vértices del lado opuesto C, se dibuja una circunferencia.

- Esta circunferencia corta a la prolongación del lado AD del cuadrado en un punto E. El segmento AE es lado mayor del rectángulo áureo ABFE, que dibujamos.

(b) Conocido el lado mayor

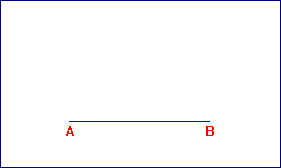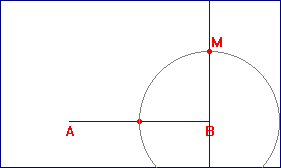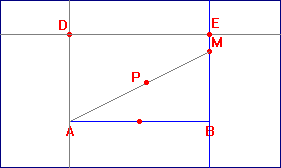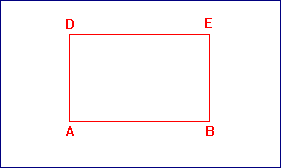
- Conocido el lado mayor AB de longitud  a. Se levanta por B un segmento perpendicular de longitud a/2, cuyo extremo nominamos M.

- Con centro en M dibujamos una circunferencia de radio MB = a/2. que corta al segmento AM en el punto P.

- La longitud de AP es el lado menor del rectángulo áureo, que dibujamos levantando por A una perpendicular y sobre ella un segmento de longitud AP.

Para construir la espiral de Durero se parte del rectángulo áureo y a su lado se construye un cuadrado de lado igual al lado mayor del rectángulo áureo con lo que se forma (con el cuadrado dibujado y el rectángulo de partida) otro rectángulo que también está en proporción áurea. Volvemos a dibujar un cuadrado cuyo lado mida la longitud del lado mayor de este último rectángulo áureo y se obtiene otro rectángulo áureo mayor, al que adosamos otro cuadrado para formar otro rectángulo áureo mayor y así sucesivamente cuantas veces deseemos. Uniendo vértices opuestos de los cuadrados adosados mediante arcos de circunferencia se obtiene la espiral.

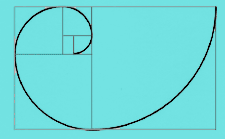
A partir de la espiral, trazando sectores y dubujando los cuadriláteros que forman los radios y la espiral se construye un mosaico en espiral :

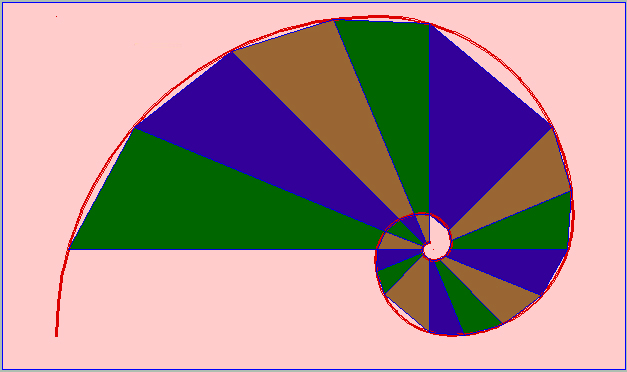
Mosaico en espiral sobre la espiral de Durero

4) Mosaico espiral basado en la espiral logarítmica

También conocida como espiral de Bernuilli porque fue quien primero la estudió a fondo (fue descubierta por Descartes).Auque pidió que se la grabara sobre su tumba en la catedral de Basilea, por error se grabó la espiral de Durero. Su ecuación en polares es r = a^q, ante la imposibilidad de dibujarla con regla y compás (necesitamos un programa de representación de funciones, vamos a usar algunas aproximaciones que sí pueden dibujarse con Geogebra .

Mosaico espiral basado en la espiral de Teodoro de Cirene

Esta espiral fue concebida por  Teodoro de Cirene

Se obtiene construyendo triángulos rectángulos sucesivos cuya hipotenusa es un cateto del siguiente, siendo el otro cateto la unidad (o una longitud constante). También pueden hacerse coincidir con los ejes de coordenadas o con distintos radios de sectores de amplitud constante.

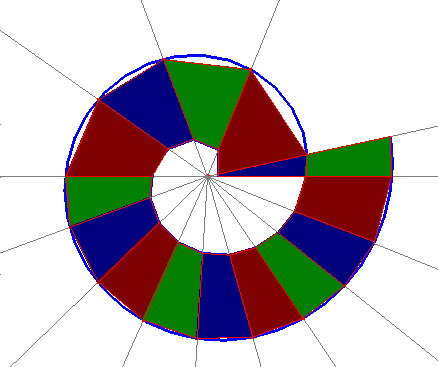
Mosaico espiral basado en la espiral de Fibonacci

La espiral de Fibonacci se puede dibujar a partir de los rectángulos de Fibonacci, que se ajustan a la sucesión de Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, ...

Comenzamos por dibujar dos cuadrados adosados cuyo lado tomaremos como longitud unidad. Estos dos cuadrados unidos forman un rectángulo de 1x2. Adosamos otro cuadrado de lado 2 obteniéndose otro rectángulo de 2x3, al que adosamos un cuadrado de lado 3 formándose un rectángulo de 3x5, por cuyo lado mayor adosamos un cuadrado de lado 5 y así sucesivamente. Uniendo los vértices opuestos de los cuadrado correspondientes a la sucesión numérica tenemos la espiral de Fibonacci :

Espiral de Fibonacci

Si ahora trazamos radios y dibujamos los cuadriláteros obtenemos el mosaico espiral basado en la espiral de Fibonacci :

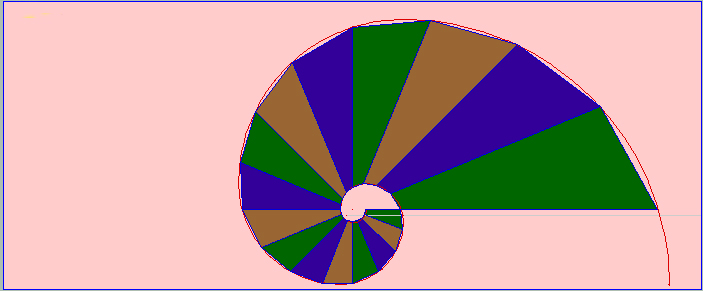
Mosaico espiral sobre la espiral de Fibonacci

Mosaico espiral basado en el triángulo de oro

Para obtener el triángulo áureo partimos del pentágono regular :

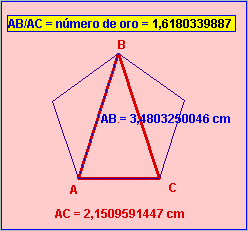
Triángulo áureo

- Si bisecamos uno de los ángulos iguales (CAB), se obtiene dos triángulo ADC y ADB. El primero también es semejante al original y por tanto áureo y el segundo también ya que AB/AD = Φ, pues AC = BD = AD.

-Podemos dibujar un arco de circunferencia con centro en D y que pase por AB.

Si bisecamos el ángulo C obtenemos E se forman otros dos triángulo áureos (AE = EC = DC) y podemos trazar otro arco de circunferencia por AC y si continuamos repitiendo el proceso se obtiene una sucesión espiral logarítmica de triángulos y arcos que converge a un punto situado en la intersección de dos medianas de los dos primeros triángulos :

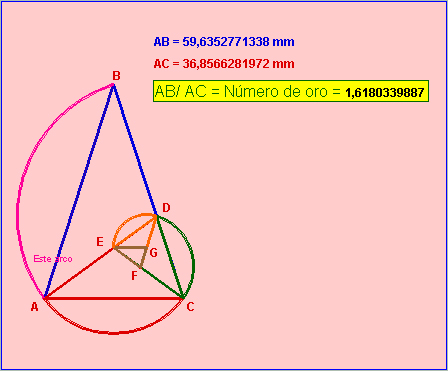
Si hallamos el centro y trazamos los radios par dividir la espiral en sectores y coloreamos los cuadriláteros que se forman tenemos el mosaicos en espiral :

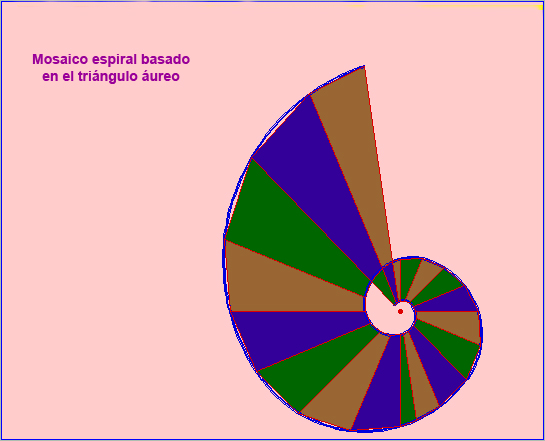
Mosaico espiral basado en el triángulo áureo

También es posible crear un espiral logarítmica degenerada consistente en circunferencias de radios exponencialmente crecientes :

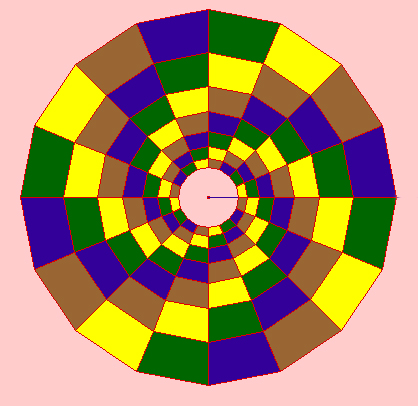
Mosaico radial exponencial

Y uniendo las diagonales de los cuadriláteros originales se obtiene un mosaico que semeja una doble espiral muy abundante en la naturaleza :

Podemos ver más sobre mosaicos espirales en esta página.