La loseta base, celda base o dominio fundamental es el motivo mínimo o baldosa más pequeña con la que se puede generar o componer el mosaico mediante isometrías.
Los términos loseta básica y dominio fundamental han aparecido en multitud de ocasiones en las páginas de los distintos tipos de mosaicos y celosías, aunque no siempre usado rigurosamente ya que, a veces, no era la loseta básica, sino el motivo mínimo que usamos para diseñar el mosaico o friso. Podía hallarse otro motivo más pequeño que nos permitiese generar el mosaico. Lo hicimos así por que para el contexto de lo que queríamos tratar nos pareció más adecuado.
Por ejemplo, cuando tratamos los mosaicos por deformación, entre los mosaicos nazaríes apareció el mosaico "hueso" :
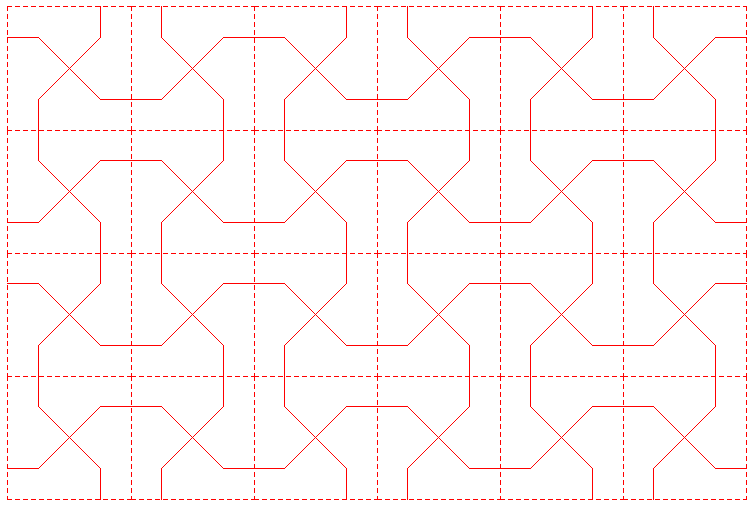
que tratamos como si su loseta básica fuese :
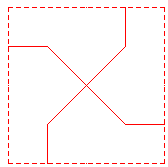
y en los frisos hemos visto que también se genera el hueso mediante :
pero en realidad, como tiene simetría rotacional de orden 4 respecto al centro del cuadrado, podemos tomar como loseta básica la cuarta parte :
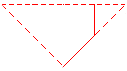
que por rotaciones de 90º, 180º y 270º genera el cuadrado y a partir del cuadrado, mediante traslaciones podemos generar el mosaico

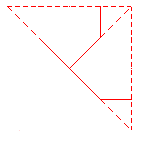
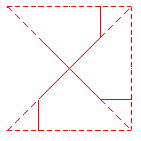
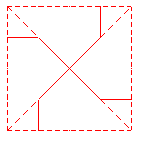
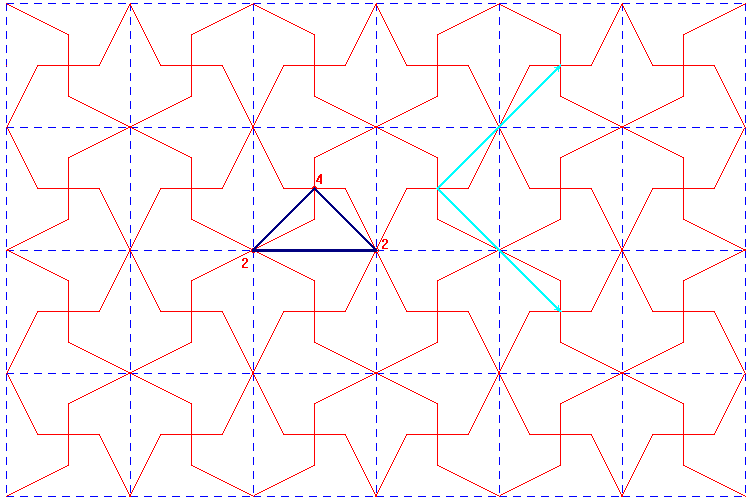
Si en el mosaico semirregular 6,4,3,4, trazamos los ejes de simetría obtenemos una figura que parece tener rejilla triangular:
luego podíamos pensar que la celda base es un triángulo como :
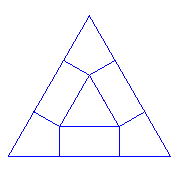
pero si nos damos cuenta de que esta figura tiene ejes de giro de orden 6, podemos considerar como baldosa base el triángulo rectángulo, sexta parte del equilátero anterior:
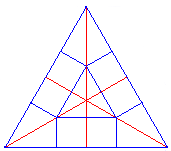
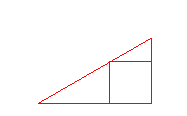
Como ves es un tema complejo que, en un principio, conviene abordar mediante la experimentación para terminar con un estudio riguroso.
En esta página tienes los ocho mosaicos semirregulares, imprímela e intenta obtener la celda base de cada uno de ellos, escribe después tu nombre y curso y entrégala a tu profesor/a.
Para realizar un estudio riguroso debes empezar por repasar, si no lo tienes claro, las isometrías del plano. En cualquier caso hay que estudiar (y dibujar a lápiz para poder corregir) las isometrías de la figura. Una vez conocidas las isometrías, y en función de ellas, conoceremos a cuál de los 17 grupos de isometrías del plano pertenece la figura y por tanto la forma de su celda base o dominio fundamental, después es cuestión de buscar una figura con esa forma que contenga las isometrías halladas. Ejemplifiquemos lo expuesto.
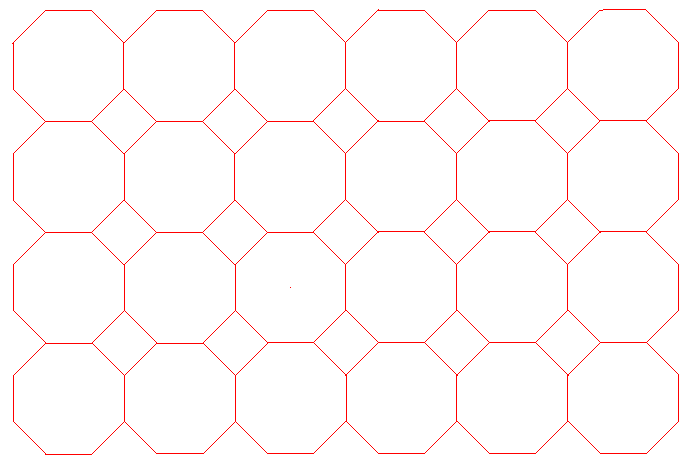
Estudiamos las isometrías y descubrimos:
° Centros de rotación de orden 4 (90º) en los centros de cada polígono.
° Centros de rotación de orden 2 (180º) en el punto medio del lado común a cada dos octógonos.
° Ejes de simetría que pasan por los centros de rotación de orden 4 y los otros 8 centros de rotación que le rodean, que forman ángulos de 45º y se cortan en el centro de giro de orden 4.
° Dos vectores de traslación perpendiculares que unen los centros de los octógonos (o los cuadrados).
° Ejes de simetría con deslizamiento.
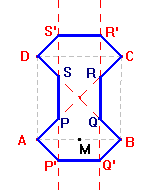
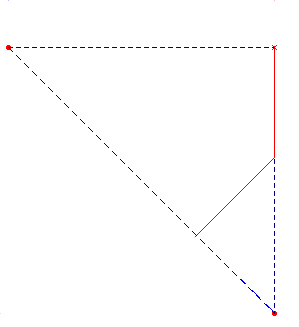
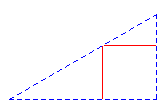
Las isometrías descubiertas indican que se trata del grupo p4m de celda base el triángulo mitad del cuadrado que se forma uniendo alternativamente dos centros de orden 2 con dos centro de rotación de orden 4:
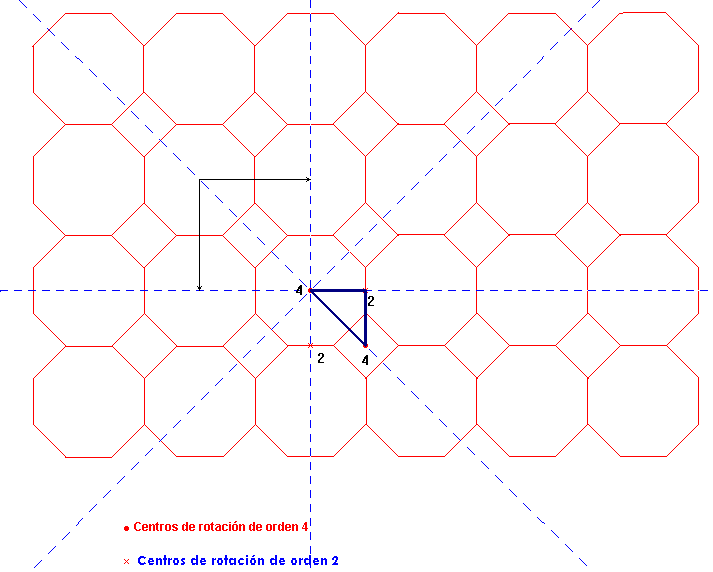
La celda base es :
Otro ejemplo :
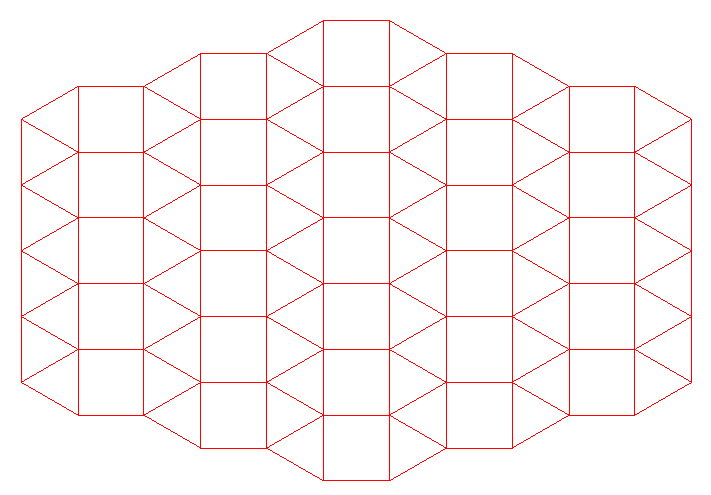
Las isometrías son :
° Centros de rotación de orden 2 (180º) en el centro de los cuadrados, en los puntos medios de los lados y en el punto medio de los lados, no comunes al cuadrado, de los triángulos.
° Ejes de simetría que pasan por los centros de rotación situados en los cuadrados.
° Dos vectores de traslación que unen los centros de rotación de los puntos medios de los lados de los cuadrados de distinta fila.
° Ejes de simetría con deslizamiento que pasan por los centro de rotación situados en los triángulos.
Las isometrías anteriores indican que se trata del grupo pmg de celda base es el triángulo rectángulo que une los centros de rotación :
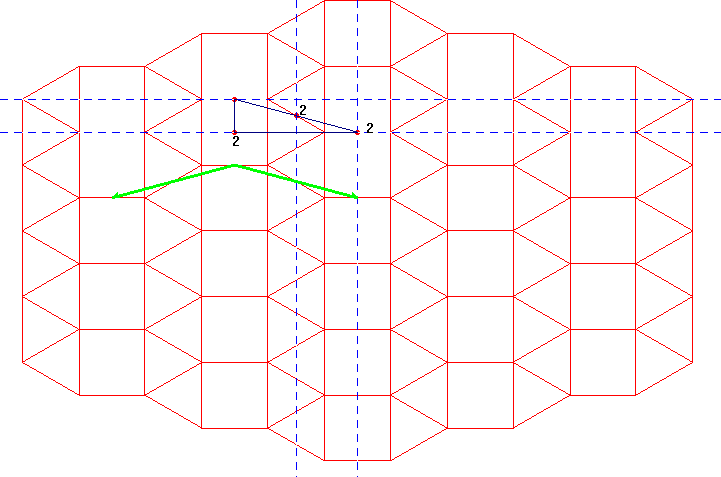
La celda base es :
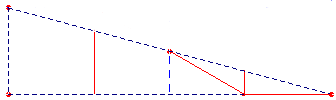
Estos ejemplos te serán de utilidad para hallar la loseta base del resto de los mosaicos semirregulares.
Un último ejemplo :
Las isometrías son:
° Centros de rotación de orden 4 en el centro de los cuadrados que forman los ejes de simetría y de orden 2 (180º) en los vértices.
° Ejes de simetría que forman una rejilla cuadrada y pasan por los centros de rotación de orden 2.
° Dos vectores de traslación perpendiculares que unen los centros de rotación de orden 4 y pasan por los de orden 2.
° Ejes de simetría con deslizamiento que pasan por los centro de rotación de orden 4.
Grupo p4m
Luego la celda base es :
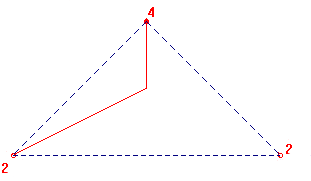
También suele ser didáctico el problema inverso, dada la baldosa base, construir el mosaico aplicando las isometrías, la secuencia para formar el 3, 4, 6,4 :
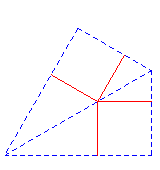
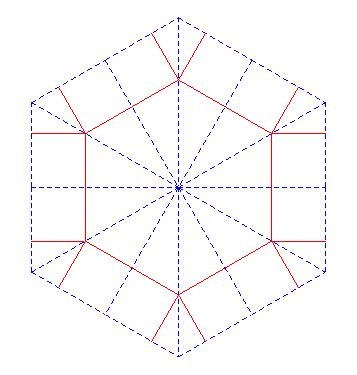
después trasladar el hexágono:
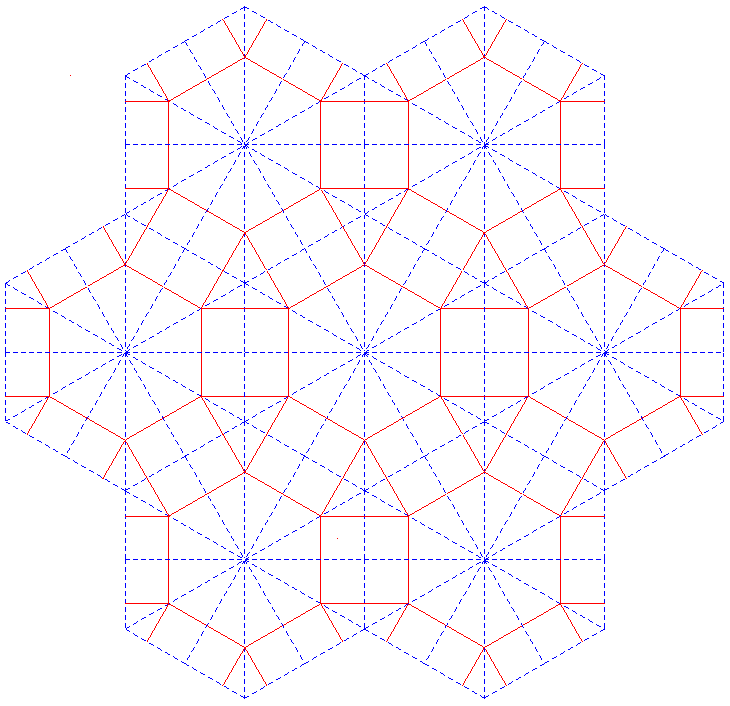
y por último, eliminar la trama :
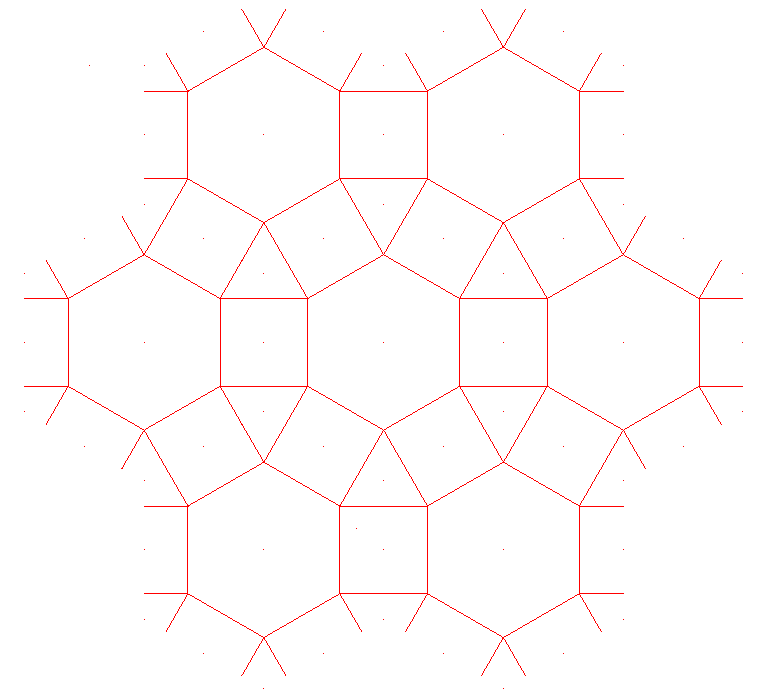
En las páginas, cuyos enlaces se muestran a continuación, realizadas con Geogebra, partiendo de algunos masaicos vamos a estudiar sus isométrías (que coracterizan al grupo isométrico que pertenecen) para determinar la celda unidad o base, que en la mayoría de los casos coincidirá con la unidad de traslación, también estudiaremos la formación del motivo mínimo y la loseta básica o dominio fundamental mediante isometrías planas aplicadas a partes de la celdilla unidad.
♠ Ejemplo de mosaico del grupo isometríco p1.
♠ Ejemplo de mosaico del grupo isométrico p2.
♠ Ejemplo de mosaico del grupo isométrico pm.
♠ Ejemplo de mosaico del grupo isométrico pg.
♠ Ejemplo de mosaico del grupo isométrico cm.
♠ Ejemplo de mosaico del grupo isométrico pmm.
♠ Ejemplo de mosaico del grupo isométrico pmg.
♠ Ejemplo de mosaico del grupo isométrico pgg.
♠ Ejemplo de mosaico del grupo isométrico cmm.
♠ Ejemplo de mosaico del grupo isométrico p4.
♠ Ejemplo de mosaico del grupo isométrico p4m.
♠ Ejemplo de mosaico del grupo isométrico p4g.
♠ Ejemplo de mosaico del grupo isométrico p3.
♠ Ejemplo de mosaico del grupo isométrico p3m1.
♠ Ejemplo de mosaico del grupo isométrico p31m.
♠ Ejemplo de mosaico del grupo isométrico p6.
♠ Ejemplo de mosaico del grupo isométrico p6m.
Los enlaces siguientes te conducen a páginas de prácticas en donde se te propone que, usando Geogebra, dibujes las isométrías que encuentres e intentes hallar un motivo mínimo que genere el mosaico, un dominio fundamental y la celdilla base. Si ya tienes Geogebra y no quieres hacer las prácticas conectado, te puedes descargar los archivos y hacer las prácticas en tu ordenador
♥ Página de prácticas del grupo de simetría p1.
♥ Página de prácticas del grupo de simetría p2.
♥ Página de prácticas del grupo de simetría pm.
♥ Página de prácticas del grupo de simetría pg.
♥ Página de prácticas del grupo de simetría cm.
♥ Página de prácticas del grupo de simetría pmm.
♥ Página de prácticas del grupo de simetría pmg.
♥ Página de prácticas del grupo de simetría pgg.
♥ Página de prácticas del grupo de simetría cmm.
♥ Página de prácticas del grupo de simetría p4.
♥ Página de prácticas del grupo de simetría p4m.
♥ Página de prácticas del grupo de simetría p3.
♥ Página de prácticas del grupo de simetría p3m1.
♥ Página de prácticas del grupo de simetría p31m.
